Scattering phase functions¶

All the scattering phase functions that can be used in the Monte Carlo simulator are implemented by subclassing xopto.mcbase.mcpf.pfbase.PfBase. The xopto.mcbase.mcpf module includes a number of commonly used scattering phase functions:

xopto.mcbase.mcpf.hg.Hg implements the Henyey-Greenstein scattering phase function
xopto.mcbase.mcpf.mhg.MHg implements the Modified Henyey-Greenstein scattering phase function
xopto.mcbase.mcpf.gk.Gk implements the Gegenbauer kernel scattering phase function
xopto.mcbase.mcpf.mgk.MGk implements the modified Gegenbauer kernel scattering phase function
xopto.mcbase.mcpf.pc.Pc implements the Power of cosine scattering phase function
xopto.mcbase.mcpf.mpc.MPc implements the Modified Power of cosine scattering phase function
xopto.mcbase.mcpf.rayleigh.Rayleigh implements the isotropic Rayleigh scattering phase function
xopto.mcbase.mcpf.lut.Lut and xopto.mcbase.mcpf.lut.LutEx implement the lookup table-based scattering phase functions that need to be used when there is no analytical inverse of the cumulative probability density function. In this case, the scattering angle cannot be sampled analytically, instead an efficient numerical sampling scheme is required.

Note

The use of Lut and LutEx is tightly coupled to the xopto.pf module that implements numerous scattering phase functions with a number of numerical utilities for computing quantifiers such as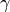 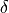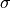$\gamma$ , $\delta$ , $\sigma$ and Legendre moments, computing the scattering cross sections of spherical particles, angular distribution of scattering probabilities, working with monodisperse, or various standard and custom size distributions, layered spherical particles, etc.

The individual scattering phase functions are conveniently imported into the xopto.mcvox.mc and xopto.mcvox.mcpf modules.

Analytical sampling¶

The following example shows how to create a Henyey-Greenstein scattering phase function with the anisotropy 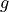$g$ set to 0.8:

from xopto.mcvox import mc

pf = mc.mcpf.Hg(0.8)

The parameters of the scattering phase function can be updated at any time through the class properties. The following examples changes the value of parameter g from 0.8 to 0.9.

pf.g = 0.9

The number and naming of parameters depends on the type of the scattering phase function. The Gegenbauer kernel scattering phase function xopto.mcbase.mcpf.gk.Gk exposes two parameters, namely gg and :code:’a’.

pf = mc.mcpf.Gk(gg=0.9, a=0.5)

Any of the two parameters can be accessed through the class properties:

pf.gg = 0.7
pf.a = 0.4

Lookup table-based numerical sampling¶

Complex scattering phase functions, such as the scattering phase functions of spherical particles that can be computed with the Mie theory, can be used with the Monte Carlo simulator through the lookup table scattering phase functions xopto.mcbase.mcpf.lut.Lut or xopto.mcbase.mcpf.lut.LutEx. In the first step we need to create an instance of a scattering phase function that enables computation of various scattering phase function quantifiers, such as the Legendre moments, 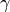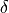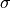$\gamma$ , $\delta$ , $\sigma$ , etc. These can be found in the xopto.pf that conveniently imports all the implemented scattering phase functions.

The following example shows how to create a Monte Carlo simulator-compatible scattering phase function xopto.mcbase.mcpf.lut.Lut() for spherical polystyrene particles of diameter 1.0 μm suspended in water and for 550 nm light. Note that we utilize the xopto.materials package from which we import the refractive index module xopto.materials.ri.

from xopto import pf
from xopto.mcvox import mc
from xopto.materials import ri

mie = pf.Mie(ri.polystyrene.default(550e-9), ri.water.default(550e-9), 1.0e-6, 550e-9)

mc_mie = mc.mcpf.Lut(*mie.mclut())

The same result can be accomplished by xopto.mcbase.mcpf.lut.LutEx() that takes the scattering phase function type and a list of arguments for the corresponding constructor (parameters of the scattering phase function).

from xopto import pf
from xopto.mcvox import mc
from xopto.materials import ri

params = [ri.polystyrene.default(550e-9), ri.water.default(550e-9), 1.0e-6, 550e-9]

mc_mie = mc.mcpf.LutEx(pf.Mie, params)

The default lookup table size is set to 2000, which should yield an accurate representation for the vast majority of the scattering phase functions. However, for scattering phase functions with an extremely high anisotropy that exceeds 0.95, a larger lookup table size might be required. The size of the lookup table can be controlled with the lutsize parameter.

from xopto import pf
from xopto.mcvox import mc
from xopto.materials import ri

params = [ri.polystyrene.default(550e-9), ri.water.default(550e-9), 1.0e-6, 550e-9]
mc_mie = mc.mcpf.LutEx(pf.Mie, params, lutsize=4000)

mie = pf.Mie(ri.polystyrene.default(550e-9), ri.water.default(550e-9), 1.0e-6, 550e-9)
mc_mie = mc.mcpf.Lut(*mie.mclut(lutsize=4000))

For scattering phase functions that come in a nonparametric form, such as when measured with a goniometer, use the xopto.pf.discrete.Discrete that can take values defined at discrete scattering angles. Then follow the above examples to obtain a Monte Carlo simulator-compatible scattering phase function with Lut() or LutEx().

Note

Any scattering phase function in xopto.pf can be converted into a lookup table-based Monte Carlo simulator-compatible scattering phase function.

The following example crates a lookup table-based implementation of the Henyey-Greenstein (Hg) scattering phase function with anisotropy 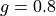$g=0.8$ :

from xopto import pf
from xopto.mcvox import mc

params = [0.8]
hg_lut = mc.mcpf.LutEx(pf.Hg, params)

The use of lookup-table based scattering phase functions in the Monte Carlo simulations will not have a notable performance impact as long as all the lookup table data can be kept in the constant memory of the OpenCL device, the size of which is for a typical GPU around 64 kB.